Continuous Numerical Values Can Take Any Value Inside an Interval

Home>AP Statistics>This page

In statistics, a variable has two defining characteristics:

• A variable is an attribute that describes a person, place, thing, or idea.
• The value of the variable can "vary" from one entity to another.

For example, a person's hair color is a potential variable, which could have the value of "blond" for one person and "brunette" for another.

Note: Your browser does not support HTML5 video. If you view this web page on a different browser (e.g., a recent version of Edge, Chrome, Firefox, or Opera), you can watch a video treatment of this lesson.

Qualitative vs. Quantitative Variables

Variables can be classified as qualitative (aka, categorical) or quantitative (aka, numeric).

• Qualitative. The value of a qualitative variable is a name or a label. The color of a ball (e.g., red, green, blue) or the breed of a dog (e.g., collie, shepherd, terrier) would be examples of qualitative or categorical variables.
• Quantitative. The value of a quantitative variable is a number. For example, when we speak of the population of a city, we are talking about the number of people in the city - a numerical attribute of the city. Therefore, population would be a quantitative variable.

In algebraic equations, quantitative variables are represented by symbols (e.g., x, y, or z).

Advertisement

Discrete vs. Continuous Variables

Quantitative variables can be further classified as discrete or continuous. If a variable can take on any value between its minimum value and its maximum value, it is called a continuous variable; otherwise, it is called a discrete variable.

Some examples will clarify the difference between discrete and continouous variables.

• Suppose the fire department mandates that all fire fighters must weigh between 150 and 250 pounds. The weight of a fire fighter would be an example of a continuous variable; since a fire fighter's weight could take on any value between 150 and 250 pounds.
• Suppose we flip a coin and count the number of heads. The number of heads could be any integer value between 0 and plus infinity. However, it could not be any number between 0 and plus infinity. We could not, for example, get 2.3 heads. Therefore, the number of heads must be a discrete variable.

Univariate vs. Bivariate Data

Statistical data are often classified according to the number of variables being studied.

• Univariate data. When we conduct a study that looks at only one variable, we say that we are working with univariate data. Suppose, for example, that we conducted a survey to estimate the average weight of high school students. Since we are only working with one variable (weight), we would be working with univariate data.
• Bivariate data. When we conduct a study that examines the relationship between two variables, we are working with bivariate data. Suppose we conducted a study to see if there were a relationship between the height and weight of high school students. Since we are working with two variables (height and weight), we would be working with bivariate data.

Test Your Understanding

Problem 1

Which of the following statements are true?

I. All variables can be classified as quantitative or categorical variables.II. Categorical variables can be continuous variables.

III. Quantitative variables can be discrete variables.

(A) I only(B) II only(C) III only(D) I and II

(E) I and III

Solution

The correct answer is (E). All variables can be classified as quantitative or categorical variables. Discrete variables are indeed a category of quantitative variables. Categorical variables, however, are not numeric. Therefore, they cannot be classified as continuous variables.

If you would like to cite this web page, you can use the following text:

Berman H.B., "Variables in Statistics", [online] Available at: https://stattrek.com/descriptive-statistics/variables URL [Accessed Date: 9/14/2022].

Here's a table that summarizes the types of variables:

Types of variables
Quantitative (a.k.a. Numerical)	Qualitative (a.k.a. Categorical)
Continuous	Discrete	Ordinal	Nominal
Consists of numerical values that can be measured but not counted.	Consists of numerical values that can be counted.	Consists of text or labels that have a logical order.	Consists of text or labels that have no logical order.
e.g. Weight {56.06 Kg, 87 Kg}	e.g. Number of disease cases {0, 1, 2, 3}	e.g. Beverage size {small, medium, large}	e.g. Profession {chemist, carpenter}

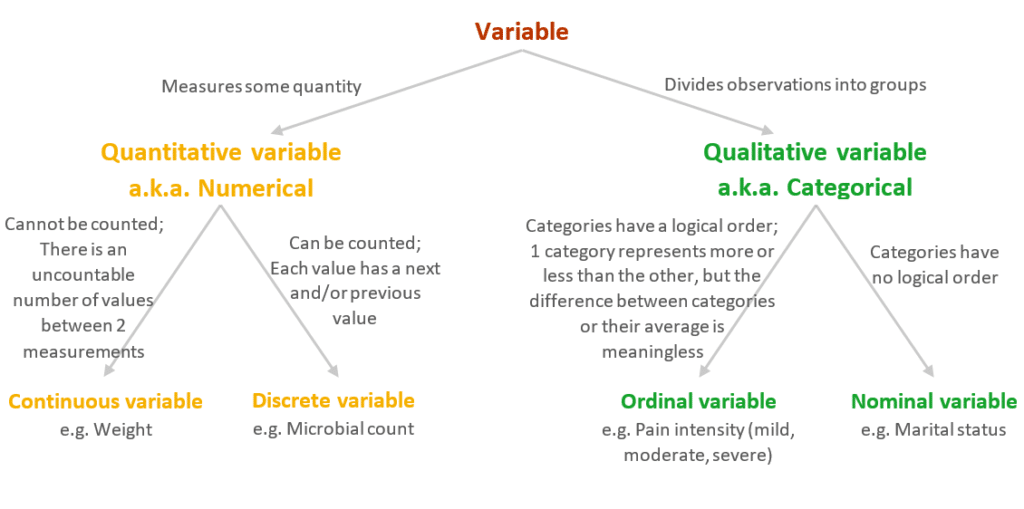
There are 2 basic types of variables: quantitative and qualitative.

1. Quantitative or Numerical variable:

A quantitative or Numerical variable is a type of variable consisting of values that represent counts or measurements of a certain quantity. For instance, age, height, number of cigarettes smoked, etc.

A quantitative variable can be either continuous or discrete.

1.1. Continuous variable:

A continuous variable is a type of quantitative variable consisting of numerical values that can be measured but not counted, because there are infinitely many values between 1 measurement and another.

Example: Cholesterol level measured in mg/dl.

1.2. Discrete variable:

A discrete variable is a type of quantitative variable consisting of numerical values that can be measured and counted, because these values are separate or distinct. Unlike a continuous variable, if you select a value at random from a discrete variable, there is a concept of next and/or previous value.

Example: Vote count in an election.

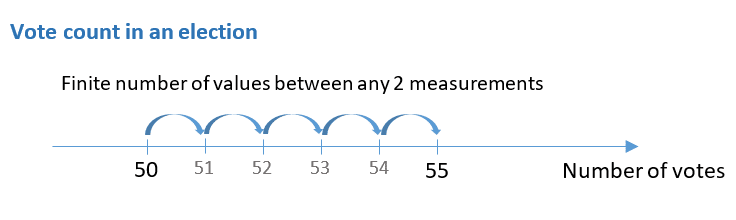
A discrete variable may take on an infinite number of values as long as they are countable (even if we would be counting forever). For instance, the "number of dice rolls until we get 2 consecutive sixes" is a discrete variable because it is countable, although we could theoretically go on forever without getting 2 sixes in a row.

⚠ Transforming text into discrete variables:
Each unique word in a group of text documents can be transformed into a discrete numerical variable whose values are the number of occurrences of the word in each of the documents. This makes possible the statistical analysis of text from sources like: comments on social media, books, research articles, etc.

In practice, all continuous variables are discrete!

Since the precision of our measurements is not infinite, a theoretically continuous variable will practically be discrete i.e. it will only take on distinct values, although very close to one another.

However, for the purpose of analyzing data, we consider a variable continuous if it can take on a very large number of possible values within a certain interval such that it would be practically impossible for 2 observations to have the same value – in other words, within a given interval, the possible values that a continuous variable can take do not have to be literally infinite.

Here are some examples to help you differentiate between discrete and continuous variables:

Exercise: Discrete or continuous?

– Is age discrete or continuous?

Age is a discrete variable when counted in years, for example when you ask someone about their age in a questionnaire. Age is a continuous variable when measured with high precision, for example when calculated from the exact date of birth.

– Is mass discrete or continuous?

Mass is a continuous variable since it can take on any value between its minimum and maximum. Mass is not discrete since there is no definite answer to the question: What is the next value for mass after, for example, 63.207 Kg?

– Is shoe size discrete or continuous?

Shoe size is a discrete variable since it takes on distinct values such as {5, 5.5, 6, 6.5, etc.}. Because there is a finite number of values between any 2 shoe sizes, we can answer the question: What is the next value for shoe size after, for example 5.5? The answer is 6 – making it a discrete variable.

– Is dosage of medicine discrete or continuous?

Dosage of medicine is a discrete variable if the medicine is administered as distinct doses of 5, 10, and 20 mg for example. Dosage of medicine is a continuous variable if the medicine is administered as a constant-rate intravenous infusion.

– Is systolic blood pressure discrete or continuous?

Theoretically, the systolic blood pressure of an individual is a continuous variable since it can take on any value between 0 and 300 mmHg. Practically, the systolic blood pressure as measured by a monitor is a discrete variable since it can only take on distinct values, such as: 140 mmHg, 141 mmHg, etc.

⚠ Half continuous and half discrete variables:
Some variables are continuous below a certain threshold and then become discrete as the accuracy of the measurements declines for larger values, such is the case with estimating of the time of death of a body. These are considered continuous variables, since it would be impossible to count all their individual values.

2. Qualitative or Categorical variable:

A qualitative or categorical variable is a type of variable consisting of text characters or labels that describe groups of observations. For instance, gender, marital status, stages of a disease, etc.

⚠ Numbers representing categorical data:
Sometimes categorical variables are coded as numbers instead of text, for instance:

• 0 and 1 to represent binary variables (e.g. Gender: where male is 0 and female is 1)
• ID numbers
• Passwords
• Phone numbers

These variables are still qualitative since their values, although numerical, do not count or measure anything, and it does not make sense to perform calculations on them. Instead, they are only used as substitutes for text.

A qualitative variable can be either ordinal or nominal.

2.1. Ordinal variable:

An ordinal variable is a type of qualitative variable consisting of text or labels that have a logical order, i.e. one category represents more or less of the other, but taking the difference between categories or their average is meaningless.

Example: Hypertension stages.

2.2. Nominal variable:

A nominal variable is a type of qualitative variable consisting of text or labels that have no logical order.

Example: Gender.

Summary: A decision tree for identifying variable type

References

• Triola M. Essentials of Statistics. 6th edition. Pearson; 2018.
• Vittinghoff E, Glidden DV, Shiboski SC, McCulloch CE. Regression Methods in Biostatistics: Linear, Logistic, Survival, and Repeated Measures Models. 2nd edition. Springer; 2011.
• Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edition. Springer; 2016.

Further reading

elmerriencrehe.blogspot.com

Source: https://paraquee.com/variables-can-take-on-any-value-in-some-interval

Share this post